1X world model challenge

an attempt at the 1X world model challenge
Resource Link
Project Repository GitHub

Ever since Sora was released, I’ve been interested in world models and how video generation captures hidden world dynamics. When 1X announced the world model challenge in June of 2024, I was extremely GPU poor and only had a 1080Ti to work with :(. Later in April of 2025, I was working with two labs at Caltech and realized I had access to two servers with 4x H100s. One of the servers was under-utilized over spring break and seeing 4x H100s at 0% utilization makes my very very sad. So I spoke to my lab mates and got access to the GPUs for the few days and started on this challenge.

Sora architecture using DiT (Diffusion Transformers)
Sora high-level architecture diagram showing the use of DiT (Diffusion Transformers) for video generation. Shows operation on spacetime patches of video and image latent codes. ([Lil'Log](https://lilianweng.github.io/posts/2024-04-12-diffusion-video/))

My first realization with world models was that they’re excellent means for data generation and eventually would become powerful simulators. Since world models learn the data distribution of the environment well, we can trace the latent space of the world model to get a sense of the world dynamics to generate data to train VLA policies. 1X started with the right approach which is evals rather than training environments since world models haven’t (yet) gotten to the point where we can train policies with accurate contact physics and dynamics.

However, after talking with Karan Dalal, one of the most cracked undergrad I’ve spoken to, I came to the realization that World Models are more capable that just being simulators. Why train a weaker model (VLA) if you have access to the data distribution that models the world? Condition world models on actions and they give you the next state prediction (Genie, DreamGen); condition world models on state and intended result to be achieved and they give you the actions to achieve that result. Then, world Models act as policies that can be used for reasoning in robotics. We’re still a long way to get anywhere close to that but mayhaps one day we might. Highly recommend the talk from Jim Fan on the Physical Turing Test where he explains how to scale data for robotics using World Models and Chris Paxton’s blog on World Models here.

Anywho, to get up to speed with the latest research in the World Model and Video Generation space, I tried to read recent papers in the field. Then I happened to stumble upon this absolute piece of art from Yen-Chen Lin. Yen-Chen is also of of the co-authors on the Nvidia COSMOS paper and I happened to trace this blog by tracing the author list on the paper. I read this blog at least 2 times and went through most of the papers he cited in the blog and kept going down the rabbit hole until I was satisfied that I had a good grasp of the field. Lillian’s blog is also a great read but I felt it was a bit too technical for beginners like me who were just learning about Video Generation and Latent Diffusion Models (LDMs). Although, I’d say that it was really helpful to go deeper into the concepts once Yne-Chen broke it down in his blog. At the time of working on this challenge, COSMOS by Nvidia was the best open-source world model and I started hacking around with the code to get a good grasp of the internals of the world model.

Here I’ll go slightly deeper into the COSMOS paper and my findings from the 1X World Model Challenge in brief. There’s a lot yet to be done and (hopefully) I’ll pick up world models again soon but I’ve shifted my focus to exploring long-horizon reasoning and generalization in VLAs for the time being.

The COSMOS World Model

The competition has two sub-challenges: Compression and Sampling, and I focused on the Compression challenge. The objective is to train a model that compresses a robot’s video and state sequences while preserving enough detail to predict future interactions.

The Compression Challenge has a specific format. Each test sample contains past latent tokens from the previous 17 video frames at 256x256 resolution, 30 fps, compressed by the Cosmos Discrete 8×8×8 tokenizer into three latent grids of shape (3, 32, 32). You also get joint-position data for the previous 17 frames plus future timesteps. Your job is to output logits for every token location in the next three latent grids - for all (3, 32, 32) tokens that encode the subsequent 17 frames.

COSMOS uses a discrete video tokenizer with an 8×8×8 compression ratio - 8× compression in the temporal dimension (every 8 frames gets compressed into 1 latent frame) and 8× compression in both height and width dimensions. This means our 17 raw video frames get mapped to a latent representation with dimensions 3×32×32, creating a total of 3,072 tokens per video clip.

The tokenizer has this temporally causal design that I found pretty clever. It uses a 2-level wavelet transform that processes inputs in a group-wise manner, starting with:

\[\{x_0, x_{1:4}, x_{5:8}, \ldots, x_{(T-3):T}\} \rightarrow \{g_0, g_1, g_2, \ldots, g_{T/4}\}\]

This transformation downsamples inputs by a factor of 4 along all dimensions, and then subsequent encoder stages process frames causally. Each stage processes current and past frames independent of future frames.

Implementation and Results

I implemented the COSMOS inference pipeline according to 1X’s specifications. For the autoregressive generation, I used the first 9 frames as conditioning context and generated the next 8 frames. In the latent space, this translates to using the first 2048 tokens (representing 9 prompt frames across 2 latent frames) as context and autoregressively generating the next 1024 tokens (representing 8 predicted frames in 1 latent frame).

More details are in the github page on how to run inference and get results.

Results

The results were suboptimal and this was sort of expected. The COSMOS 1-4B model was originally trained using an 8×16×16-720p tokenizer, while the 1X validation dataset uses an 8×8×8 tokenizer. I later realized that I could have fixed this by resizing and padding the videos to the data resolution it was trained on, tokenized on that resolution, run inference and then resized and unpadded the output tokens back to the required token resolution. This might have given me better performance but again, the resized data would be OOD so I’m not sure how well COSMOS would generalize without SFT.

Results with 8×8×8 Tokenizer

Sample 1 tokenized
Sample 11 tokenized
Sample 13 tokenized
Sample 24 tokenized
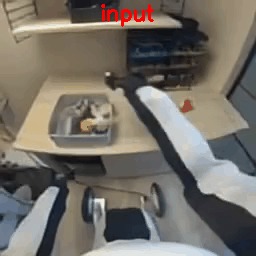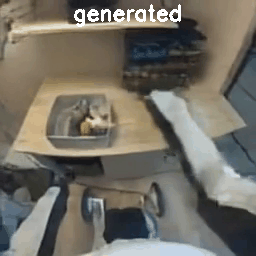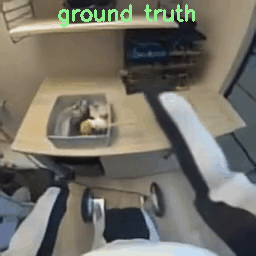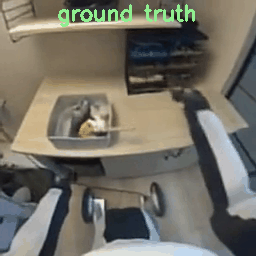
Sample 40 tokenized
Sample 72 tokenized
Sample 162 tokenized
Sample 248 tokenized
Results with 8×8×8 tokenizer showing suboptimal quality due to tokenizer mismatch.

To verify the mismatch theory, I re-ran the process but encoded the raw videos on the fly using the model’s native 8x16x16 tokenizer. They show better quality since they match COSMOS’s data distribution.

Sample 17 raw
Sample 2 raw
Sample 20 raw
Sample 23 raw
Sample 27 raw
Sample 33 raw
Sample 36 raw
Sample 9 raw
Results with native 8×16×16 tokenizer showing improved quality matching COSMOS's training distribution.

Evaluation Methodology

For evaluation, I calculated cross-entropy loss averaged across all 8 generated frames. The approach was:

# Extract the relevant logits for frames being predicted
future_logits = generation_logits[0, :ground_truth_future_tokens.size(0), :]  # [seq_len, vocab_size]
        
# Calculate cross entropy between model predictions and ground truth
ce_loss = F.cross_entropy(future_logits, ground_truth_future_tokens).item()

I’m not entirely sure if this captures the temporally teacher-forced loss that the challenge expects, but it gives us a reasonable metric for comparing model performance across different configurations.

Technical Deep Dive: Video Tokenization in COSMOS

The 8×8×8 Compression Architecture

The Cosmos model uses a discrete video tokenizer with 8×8×8 compression:

Given this compression ratio, a sequence of 17 raw video frames results in a latent representation with dimensions:

$T_{latent} \times H_{latent} \times W_{latent} = \lceil 17/8 \rceil \times H/8 \times W/8 = 3 \times 32 \times 32$

This creates a total of 3×32×32 = 3,072 tokens per video clip. For 256×256 input frames, each latent frame is represented as a 32×32 grid of tokens.

Inference with Pre-trained Autoregressive Models

The inference operates in a fully autoregressive scenario with:

Token Organization

For a 17-frame sequence tokenized to 3 latent frames:

$\text{Tokens} = [t_1, t_2, …, t_{2048} \text{ (9 prompt frames, 2 latent frames)}, t_{2049}, …, t_{3072} \text{ (8 predicted frames, 1 latent frame)}]$

In the latent grid layout (3×32×32):

This is because the groups are formed such that the first frame is downsampled in a temporally causal manner to the first latent frame. The paper doesn’t explicitly mention this, but my assumption is that this helps in retrieving more information from the first frame as context.

The tokenizer compresses the temporal dimension from $(1 + T)$ raw frames to $(1 + T’)$ latent frames, where:

$T’ = \lceil T/8 \rceil$

So, the 17-frame sequence is compressed to 3 latent frames.

COSMOS Tokenization Process
COSMOS Tokenization Process.

Causal Temporal Design

The tokenizer uses a temporally causal design so that each stage processes only current and past frames, independent of future frames. So for the 8×8×8 tokenized dataset given, it was safe to extract the first 2048 tokens representing the first 9 frames as context and then autoregressively generate the next 1024 tokens representing the next 8 frames since the encoding for the first 9 frames is not polluted by future frames.

The Tokenization Process

The tokenization begins with a 2-level wavelet transform that processes inputs in a group-wise manner:

${x_0, x_{1:4}, x_{5:8}, \ldots, x_{(T-3):T}} \rightarrow {g_0, g_1, g_2, \ldots, g_{T/4}}$

This transformation downsamples inputs by a factor of 4 along all dimensions (x, y, t) and then subsequent encoder stages process frames in a temporally causal manner:

${g_0, g_{0:1}, g_{0:2}, \ldots} \rightarrow {\xi_0, \xi_1, \xi_2, \ldots}$

Reflections

I think world models are extremely powerful tools for robotics and data generation but I also do think there’s a lot of hype around them. Genie 3 videos certainly did make me question this opinion but I still think there’s a lot more work to be done for robotics because of how little data is available to train world models with. I do strongly think that most Genie 3 videos were cherry picked and not a lot was revealed on its performance OOD which is why I’m being a skeptic here but it’s not to say that world models are not powerful. Working on this challenge gave me a much deeper appreciation for the complexity of video generation models. I did learn a lot about LDMs, DiTs and tokenizers and will continue to explore this space.

The 4x H100s didn’t go to waste after all :)

If you’re interested in diving deeper into world models or want to build upon this work, all the code is available on my GitHub repository. Feel free to reach out if you have questions or hack together something cool in this space :)